蒙特卡洛（Monte Carlo）模拟是一个重要的科学工具，它被广泛地应用于高能物理、凝聚态物理、高分子物理以及其他许多复杂系统的科学研究。然而，大多数现有的蒙特卡洛算法由于“临界慢化”在临界点附近变得效率很低。邓友金教授长期工作在新型团簇(cluster)算法，虫子(worm)，以及Sweeny算法的设计和发展。与纽约、巴黎以及马德里的一些同事一起，邓友金教授和学生黄远应用解析分析、蒙特卡洛算法和转移矩阵等方法在研究一些在统计物理以及凝聚态物理占重要地位的晶格模型取得新进展。该研究成果发表在《美国物理评论快报》[Phys. Rev. Lett. 107, 150601 (2011)]上。
　　邓友金教授研究组在一类欧拉平面的三角类晶格上，研究了四态反铁磁Potts模型；在零温下，这也是人们常说的四色模型。 通过一些解析的分析，他们判断，只要某个子晶格的格点配位数为四，系统将在非零温的时候有一个相变。研究组预测了相变的普适类。然后，研究组应用蒙特卡洛和转移矩阵方法模拟了union-jack及bisected hexagonal晶格，并证实了研究组的预测。邓友金教授研究组的研究表明，在非零熵密度的系统中，长程序有可能在系统的某些子晶格自发产生。这对统计物理中熵和有序之间的关系，提供了一个新视角。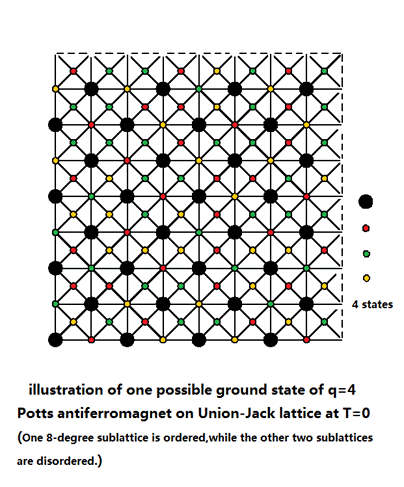
参考文献：
Finite-temperature phase transition in a class of four-state Potts antiferromagnets
Youjin Deng; Yuan Huang; Lykke Jacobsen, J.; Salas, J.; Sokal, A.D.
Physical Review Letters（2011） DOI: 10.1103/PhysRevLett.107.150601